Curso de Microcontroladores PIC

Entra y aprende a programar con Microcontroladores

Link del Curso de Microcontroladores

PROGRAMACIÓN DE MÉTODOS NUMÉRICOS EN SCILAB

Bienvenidos a este nuevo espacio donde aprenderemos a resolver las raíces de las ecuaciones mediante métodos numéricos utilizando el método analítico y el programa scilab.

QUE ES SCILAB?

Scilab es un software matemático, con un lenguaje de programación de alto nivel, para cálculo científico, interactivo de libre uso y disponible en múltiples sistemas operativos (Mac OS X, GNU/Linux, Windows). Desarrollado por INRIA (Institut National de Recherche en Informatique et en Automatique) y la ENPC (École Nationale des Ponts et Chaussées) desde 1990, por Scilab Consortium dentro de la fundación Digiteo desde 2008, Scilab es ahora desarrollado por Scilab Enterprises desde julio 2012.

Scilab fue creado para hacer cálculos numéricos aunque también ofrece la posibilidad de hacer algunos cálculos simbólicos como derivadas de funciones polinomiales y racionales. Posee cientos de funciones matemáticas y la posibilidad de integrar programas en los lenguajes más usados (Fortran, Java, C y C++). La integración puede ser de dos formas: por ejemplo, un programa en Fortran que utilice Scilab o viceversa. Scilab fue hecho para ser un sistema abierto donde el usuario pueda definir nuevos tipos de datos y operaciones entre los mismos.

Scilab viene con numerosas herramientas: gráficos 2-D y 3-D, animación, álgebra lineal, matrices dispersas, polinomios y funciones racionales, Simulación: programas de resolución de sistemas de ecuaciones diferenciales (explícitas e implícitas), Xcos: simulador por diagramas en bloque de sistemas dinámicos híbridos, Control clásico, robusto, optimización LMI, Optimización diferenciable y no diferenciable, Tratamiento de señales, Grafos y redes, Scilab paralelo empleando PVM, Estadísticas, Creación de GUIs, Interfaz con el cálculo simbólico (Maple, MuPAD), Interfaz con TCL/TK.

Además se pueden agregar numerosas herramientas o toolboxes hechas por los usuarios como Grocer una herramienta para Econometría u Open FEM (Una caja de Herramientas para Elementos Finitos), hecha por INRIA.

                                          

                                           CLICK PARA DESCARGAR SCILAB 5.4.1

MÉTODOS CERRADOS

Para resolver las  raíces de ecuaciones se ocupa de métodos que aprovechan el hecho de que una función cambia de signo en la vecindad de una raíz. A estas técnicas se les llama métodos cerrados, o de intervalos, porque se necesita de dos valores iniciales para la raíz. Como su nombre lo indica, dichos valores iniciales deben "encerrar", o estar a ambos lados de la raíz. Los métodos particulares descritos aquí emplean diferentes estrategias para reducir sistemáticamente el tamaño del intervalo y así converger a la respuesta correcta.

Como preámbulo de estas técnicas se analizarán los métodos gráficos para representar tanto las funciones como sus raíces. Además de la utilidad de los métodos gráficos para determinar valores iniciales, también son útiles para visualizar las propiedades de las funciones y el comportamiento de los diversos métodos numéricos.

MÉTODO DE LA BISECCIÓN

Cuando f(x) cambió de signo a ambos lados de la raíz. En general, si f(x) es real y continúa en el

intervalo que va desde xl hasta x_u y f(x1) y f(x_u) tienen signos opuestos, es decir:

                                                      f(x1),f(xu)< 0     

                      

Entonces hay al menos una raíz real entre x1 y x_u.

Los métodos de búsqueda incremental aprovechan esta característica localizando un intervalo en el que la función cambie de signo. Entonces, la localización del cambio de signo (y, en consecuencia, de la raíz) se logra con más exactitud al dividir el intervalo en varios subintervalos. Se investiga cada uno de estos subintervalos para encontrar el cambio de signo. El proceso se repite y la aproximación a la raíz mejora cada vez más en la medida que los subintervalos se dividen en intervalos cada vez más pequeños.

El método de bisección, conocido también como de corte binario, de partición de intervalos o de Bolzano, es un tipo de búsqueda incremental en el que el intervalo se divide siempre a la mitad. Si la función cambia de signo sobre un intervalo, se evalúa el valor de la función en el punto medio. La posición de la raíz se determina situándola en el punto medio del subintervalo, dentro del cual ocurre un cambio de signo. El proceso se repite hasta obtener una mejor aproximación. 

EJEMPLO

Determine las raíces reales de la  función f(x)= (0.8-0.3x)/x.
Utilice el método de la bisección para localizar la raíz más pequeña. Use los valores iniciales xa= 1 y xb=3 con un error máximo de 0.1.

DATOS 

xa=1  (Limite inferior de la función xi)

xb=3 (Limite superior de la función xs)

error anterior = 0

emax=0.1

MÉTODO ANALÍTICO

Primera Iteracción

xr=(xa+xb)/2

xr=(1+3)/2

xr=2

error=|(xr-error anterior)/xr|* 100%

error=|(2-0)/2|*100%

error=100%

Segunda Iteracción

xr=(2+3)/2

xr=2.5

error=|(2.5-2)/2.5|*100%

error=20%

Tercera Iteracción

xr=(2.5+3)/2

xr=2.75

error=|(2.75-2.5)/2.75|*100%

error=9.09091%

Cuarta Iteracción

xr=(2.5+2.75)/2.5

xr= 2.625

error=|(2.625-2.75)/2.625|*100%

error=4.76190%

Quinta Iteracción

xr=(2.625+2.75)/2.625

xr= 2.68750

error=|(2.68750-2.625)/2.68750|*100%

error=2.32558%

Sexta Iteracción

xr=(2.625+2.68750)/2.625

xr= 2.65625

error=|(2.65625-2.68750)/2.65625|*100%

error=1.17647%

Septima Iteracción

xr=(2.625+2.68750)/2.625

xr= 2.67188

error=|(2.67188-2.65635)/2.67188|*100%

error=0.58480%

Octava Iteracción

xr=(2.625+2.67188)/2.625

xr= 2.66406

error=|(2.66406-2.67188)/2.66406|*100%

error=0.29326%

Novena Iteracción

xr=(2.66406+2.67188)/2.66406

xr= 2.66797

error=|(2.66797-2.66406)/2.66797|*100%

error=0.14641%

Decima Iteracción

xr=(2.66406+2.66797)/2.66406

xr= 2.66602

error=|(2.66602-2.66797/2.66602|*100%

error=0.07326%

UTILIZANDO EL PROGRAMA SCILAB 

Realizaremos a continuación estos sencillos pasos.
1) Debemos de tener instalado el programa de scilab en nuestro ordenador....
2) Luego de descargar y descomprimir el programa, procedemos a abrir el archivo Bisección_caso1.sce

3) Nos aparecerá una pantalla como se muestra a continuación.

4) Hacemos click en Ejecutar archivo sin eco....

5) Finalmente nos saldrá una pantalla como se muestra a continuación......

Donde  nos pedirá ingresar la función f(x), el límite Inferior xa, el límite Superior xb y el error Máximo emax como parámetros..... En este caso tomaremos los datos del ejemplo de arriba. 

Gráfica Error vs Iteracción 

Nota: 

-Prueba con otras funciones f(x) no solo con las que te mostramos en el ejemplo. 

-Recuerda al momento de ingresar el limite inferior y el limite superior debes ser un intervalo que contenga a la raíz,  

-Si te descargas Método de la Bisección por error, el error será la variable a  que controle el programa, si por el contrario encojes Método de la Bisección por iteracción será logico que ahora nuestra variable será controlada por la iteracción.

!Espero que te sirva de mucha ayuda!.

                           CLICK AQUI PARA DESCARGAR MÉTODO BISECCIÓN POR ERROR

                          CLICK AQUI PARA DESCARGAR MÉTODO BISECCIÓN POR ITERACCIÓN 

LINKS DE INTERÉS 

• Métodos Numéricos para Ingenieros – Steven Chapra, Raymond P. – 5ta

                                             CLICK AQUI PARA DESCARGAR EL LIBRO

• Manual en español de Programación Scilab 

                                CLICK AQUI PARA DESCARGAR EL MANUAL DE SCILAB

Como construir una Punta Lógica de Siete Segmentos

A continuación presentaremos un informe de como se realiza una punta lógica de 7 segmentos para comprobar los estados lógicos que son el 0 y el 1 lógico.

1. TEMA:

Punta lógica de siete segmentos

2. OBJETIVOS:

✔ Construir una punta lógica de siete segmentos

✔ Comprobar el funcionamiento de la punta lógica

3. MATERIALES Y EQUIPOS:

1 circuito integrado 47ls04

1 display de 7 segmentos ánodo común

1 transistor NPN 203904

1 resistencia de 1 kΩ

1 resistencia de 10 kΩ

1 resistencia de 470 Ω

5 resistencias de 220 Ω

1 base para CI de 14 pines

Terminales para circuito impreso

1 punta de prueba

1 caja de montaje

Placa de baquelita

Acido férrico


4. MARCO TEÓRICO

Circuito integrado 74LS04

La compuerta NOT es una puerta lógica digital que implementa la negación lógica. Cuando su entrada está en 0 (cero) o en BAJA, su salida está en 1 o en ALTA, mientras que cuando su entrada está en 1 o en ALTA, su SALIDA va a estar en 0 o en BAJA.

Se puede ver claramente que la salida X solamente es "1" (1 lógico, nivel alto) cuando la entrada A está en "0" o en BAJA, mientras que la salida X solamente es "0" (0 lógico, nivel bajo) cuando la entrada A está en "1" o en ALTA.

Esta situación se representa en álgebra booleana como: X = (-A)

La representación circuital es con un solo pulsador normal cerrado, conectado en circuito simple. Una proposición lógica que corresponde a una compuerta NOT es la siguiente: Las compuertas Lógicas NOT o INVERSORA se fabrican de una sola entrada.

Transistor NPN 2N3904

El transistor 2N3904 es uno de los más comunes transistores NPN generalmente usado para amplificación. Está diseñado para funcionar a bajas intensidades, bajas potencias, tensiones medias, y puede operar a velocidades razonablemente altas. Se trata de un transistor de bajo costo, muy común, y suficientemente robusto como para ser usado en experimentos electrónicos.

Es un transistor de 200 miliamperios, 40 voltios, 625 milivatios, con una Frecuencia de transición de 300 MHz, con una beta de 100. Es usado primordialmente para la amplificación analógica.

Display de 7 segmentos ánodo común

El display de 7 segmentos o visualizador de 7 segmentos es un componente que se utiliza para la representación de números en muchos dispositivos electrónicos debido en gran medida a su simplicidad. Aunque externamente su forma difiere considerablemente de un diodo LED (diodos emisores de luz) típico, internamente están constituidos por una serie de diodos LED con unas determinadas conexiones internas, estratégicamente ubicados de tal forma que forme un número 8.

A cada uno de los segmentos que forman el display se les denomina a, b, c, d, e, f y g y están ensamblados de forma que se permita activar cada segmento por separado consiguiendo formar cualquier dígito numérico.

Descripción de la punta lógica

Una punta lógica es un instrumento que detenta la presencia de niveles altos y bajos o de señales de pulsos ene cualquier circuito digital.

Estas condiciones se pueden visualizar en leds o displays. Un display es un paquete de 7 leds dispuestos de forma de 8 que se iluminan para visualizar números y otros caracteres

En la siguiente figura se visualiza el diagrama esquemático de la punta lógica. El estado lógico (0,1 y pulsos) del punto bajo prueba se visualiza se visualiza en el display de 7 segmentos. Cada uno de los segmentos se ilumina cuando su ando e positivo respecto al catado.

Para su análisis el circuito se puede dividir en dos etapas H y L en el diagrama. Cada una de ellas realiza una función específica dependiendo del tipo de señal de entrada.

La etapa H procesa e indica la condición alta o de 1 lógico. La etapa L indica la condición baja o de 0 lógico.

5. DESARROLLO

a. Armar el circuito de la figura 1 en un protoboard y probar.

b. Simular el circuito utilizando el software Proteus ISIS

c. Convertir el circuito de la simulación a Proteus ARES

d. Imprimir el circuito impreso en una hoja de papel foto transferible

e. Transferir el circuito a una placa de baquelita

f. Revelar las pistas del circuito utilizando una solución de ácido férrico

g. Comprobar la continuidad de cada una de las pistas

h. Limpiar el circuito PCB revelado

i. Soldar cada uno de los elementos teniendo en cuenta la disposición de los mismos

j. Montar el circuito PCB terminado en una caja y conectar los cables de alimentación y la punta de prueba.

6. ANÁLISIS DE RESULTADOS

· Cuando el punto es bajo, por efecto de un bajo en la entrada de prueba, los segmentos a, b, g y f se iluminan mostrando el número 0. 

· Cuando se aplica un alto al ala entrada el transistor Q1 recibe un alto en su base a través de R2 y conduce aplicando un alto a la entrada de buffer C-D. Este último suministra un bajo al segmento e y lo ilumina. 

· Cuando se aplica una señal de pulsos a la entrada, sucede alternadamente los dos casos anteriores, se iluminan los segmentos a, b, f, g y e en el display y se forma la letra P, que significa pulsos. 

· Cuando no se aplica señal alguna a la entrada del transistor Q1 no conduce, suministra un bajo al buffer D-E y este aplica un alto al segmento e. por esta razón no se ilumina. Al mismo tiempo el inversor A interpreta su entrada al aire como 1 en alto, entrega un valor al buffer B-C y este aplica un alto a los segmentos a, b, f y g, estos tampoco se iluminan.

1. 

2. 

3. 

4. 

5. 

7. CONCLUSIONES

· Se construyó una punta lógica con visualizar de 7 segmentos la cual muestra un valor de 1 si el circuito se encuentra en buen estado, un 0 si no existe voltaje en el mismo y una letra P que nos indica que la salida existe pulsos. 

· El transistor actúa como interruptor permitiendo que no exista un 0 o un 1 a la vez en el display de 7 segmentos. 

· La letra P se muestra en el display por la razón que a la entrada se aplica una señal de pulsos que activa o desactiva la base del transistor de manera alternada. 

8. RECOMENDACIONES

· Comprobar la continuidad de las pistas para evitar problemas de funcionamiento

· Tener en cuenta la disposición de elementos antes de soldarlos

9. BIBLIOGRAFÍA

✔ http://es.wikipedia.org/wiki/Visualizador_de_siete_segmentos Consultado el 03/11/2013

✔ http://es.wikipedia.org/wiki/Puerta_NOT Consultado el 03/11/2013

✔ Curso de electrónica digital cekit

10. ANEXOS

CLICK AQUI PARA DESCARGAR EL DISEÑO EN PROTEUS

CLICK AQUI PARA DESCARGAR EL INFORME EN FORMATO WORD 

FELIZ NAVIDAD

"La navidad es el calor que vuelve al corazón de las personas, la generosidad de compartirla con otros y la esperanza de seguir adelante", de parte de Proyectos Libros Solucionarios Espe-L te deseamos una ''Feliz Navidad'' y un Prospero "Año Nuevo 2014 ", que Dios bendiga cada una de  nuestras  familias y hogares, que este nuevo Año sea lleno de Triunfos y Éxitos en cada una de nuestras vidas.

MECANISMOS LEY DE GRASHOF

Evidentemente, una de las consideraciones de mayor importancia cuando se diseña un mecanismo que se impulsará con un motor, es asegurarse de que la manivela de entrada pueda realizar una revolución completa. Los mecanismos en los que ningún eslabón describe una revolución completa no serían útiles para estas aplicaciones.

Cuando se trata de un eslabonamiento de cuatro barras, existe una prueba muy sencilla para saber si se presenta este caso.

La ley de Grashof afirma que, para un eslabonamiento plano de cuatro barras, la suma de las longitudes más corta y m ás larga de los eslabón es no puede ser mayor que la suma de las longitudes de los dos eslabones restantes, sí se desea que exista una rotación relativa continua entre dos elementos. Esto se ilustra en la

figura 1-9, en donde el eslabón más largo tiene la longitud 1, la del más corto es s y los otros dos tienen las longitudes p y q. Siguiendo esta notación, la ley de Grashof especifica que uno de los eslabones, en particular el más pequeño, girará continuamente en relación con los otros tres sólo cuando

                                                            s+l<p+q

Si no se satisface esta desigualdad, ningún eslabón efectuará una revolución completa en relación con otro.

Conviene hacer notar el hecho de que nada en la ley de Grashof especifica el orden en el que los eslabones se conectan, o cuál de los eslabones de la cadena de cuatro barras es el fijo. En consecuencia, se está en libertad de fijar cualquiera de los cuatro que se crea conveniente. Cuando se hace ésto se crean las cuatro inversiones del eslabonamiento de cuatro barras ilustrado en la figura 1-9. Las cuatro se ajustan a la ley de Grashof y en cada una de ellas el eslabón s describe una revolución completa en relación con los otros eslabones. Las diferentes inversiones se distinguen por la ubicación del eslabón s en relación con el fijo.

Si el eslabón más corto s es adyacente al fijo, como se consigna en la figura 1-9a y b, se obtiene lo que se conoce como eslabonamiento de manivela-oscilador.

Por supuesto, el eslabón s es la manivela ya que es capaz de girar continuamente, y el eslabón p, que sólo puede oscilar entre ciertos limites, es el oscilador. El mecanismo de eslabón de arrastre, llamado también eslabonamiento de doble manivela. se obtiene seleccionando al eslabón más corto s como el de referencia.

En esta inversión, que se muestra en la figura 1-9c, los dos eslabones adyacentes a s pueden girar en forma continua y ambos se describen adecuadamente como manivelas y, por lo común, el más corto de los dos se usa como entrada. Aunque se trata de un mecanismo muy común, el lector descubrirá que es un problema muy interesante intentar construir un modelo práctico que pueda operar un ciclo completo.

Si se fija el eslabón opuesto a s, se obtiene la cuarta inversión, o sea, el mecanismo de doble oscilador que aparece en la figura 1-9d. Se observará que aunque el eslabón s es capaz de efectuar una revolución completa, ninguno de los adyacentes al de referencia puede hacer lo mismo, ambos deben oscilar entre límites y son, por lo tanto, osciladores.

En cada una de estas inversiones, el eslabón más corto s es adyacente al más largo l. No obstante, se tendrán exactamente los mismos tipos de inversiones del eslabonamiento si el eslabón más largo l está opuesto al más corto s; el estudiante debe demostrar esto para comprobar que así es en efecto.

PARTES DE UN MECANISMO DE 4 BARRAS

s=Manivela

l=Biela

p=Balancín

q=Bastidor o Carcaza

EJEMPLO

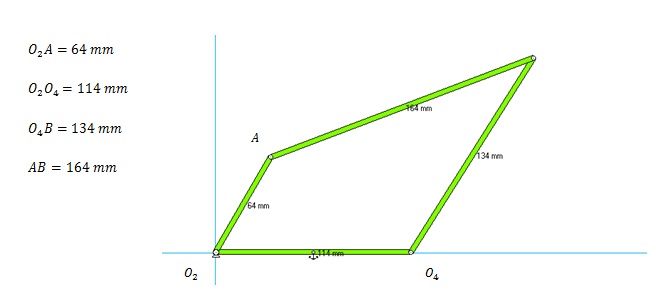
Determine si el siguiente mecanismo cumple con la ley de Grashof, dibuje el mecanismo

 s+l<p+q

64 mm+164 mm < 134 mm+114 mm

228 mm < 248 mm

Si cumple con la ley de Grashof el eslabón motriz se da la vuelta o cumple un periodo completo

TIPOS DE INVERSIÓN EN 4 BARRAS SIMULACIONES EN WORKING MODEL 

a) Mecanismo manivela y oscilador

b) Mecanismo manivela y oscilador

c) Mecanismo doble manivela

d) Mecanismo doble oscilador o eslabón